|
Андрей ПУЗИКОВ Калининград, январь, 2015 г.
Физика Беспредельности
В развитие данной темы автором написана новая редакция книги "Физика Беспредельности 2", в которой тема значительно углублена, а также исправлены некоторые ошибки.
Часть 1
Часть 2
Часть 3
1. Введение
То, что мир, в котором мы существуем, организован по определенным правилам, никем не подвергается сомнению. Однако, относительно причины возникновения этих правил мнения людей расходятся. Кто-то предпочитает относить эти правила к компетенции бога-создателя. Кто-то воспринимает их как некую самосуществующую и независящую от субъектов реальность. Но и в том и в другом случае мы имеем дело с осознанной или неосознанной концепцией ограниченности области, в которой данные правила действуют. Любое правило, любой закон ограничивает сам себя и сам для себя определяет область своего действия. И, естественно, за границами своей определенной области применения ни одно правило и ни один закон не действуют.
Но, казалось бы, какое нам дело до той неопределенной абстракции, которая находится где-то за пределами воспринимаемого нами реального мира? Достаточно понять и изучить все те правила и законы, от которых зависит комфорт нашего бытия, и научиться ими грамотно пользоваться. В пределах законов физического мира этим занимается физика, но, опять-таки - в пределах. А всегда ли наше бытие и его комфортность остается в этих пределах? И ни один грамотный физик не станет утверждать, что законы физики полностью исчерпывают собой все законы реальности.
И, все-таки, желание понять то, что находится там, за всеми пределами, не праздное любопытство. Можно долго и кропотливо изучать окружающую реальность изнутри, методом проб и ошибок, постановки целенаправленных экспериментов и совершенствовать на основе полученных результатов физические теории, но можно пойти и другим путем - попытаться понять, как эта окружающая нас реальность возникает в том, что находится за ее пределами. Осознав сам принцип, мы сможем не только гораздо глубже и точнее раскрыть все законы нашего бытия, но и понять тенденции их эволюционного изменения в глобальной динамике космических процессов.
Над каждой ограниченной областью со своими внутренними законами существует более глобальная область, в которой существует более общий, глобальный закон, определяющий существование внутри него ограниченных областей со своими частными законами. Но тогда, если последовательно выходить за пределы все дальше и дальше, мы должны непременно придти к некоему единому всё объединяющему закону... На этом месте формальная логика фатально буксует. Наличие любого определенного закона есть ограничение, а значит, за него снова можно выйти. Определить каким-то образом то, что включает в себя всё и выходит за все пределы, невозможно в рамках формальной логики. Само по себе, это не проблема, но проблема возникает тогда, когда мы пытаемся понять и выстроить логику возникновения законов нашего физического мира в этом глобальном нечто. Сомневаться в строгом соответствии физических законов формальной логике нет никаких оснований, но только в определенных рамках наших практических возможностей непосредственного восприятия окружающего мира. Более того, формальная логика вторична к законам физической реальности и являет собой абстрагировано-обобщенное их отражение. Но в этом как раз и содержится ключ к решению проблемы. Формальная логика является частной редукцией, следствием некоей более глобальной логики, проекцией ее в наш мир, где мы каким-то образом обрели свое бытие.
Остается только согласиться с тем, что формальная логика не годится для осознания и понимания глобальных принципов бытия, но это не означает, что мы должны совсем от нее отказаться. Формальная логика верна, но только как частная проекция в наш мир глобальной логики, и действует правильно в границах нашего локального мира. Но разве мы не можем по этой проекции попытаться понять саму глобальную логику?
Именно это я попытался сделать, и получил результат, превышающий все, даже самые фантастические ожидания. Все известные законы физики не просто выстраиваются “сверху” всего из одного глобального принципа, не просто наполняются смыслом, но и дополняются новыми, неизвестными до этого, сочетаниями и формулами.
Предлагаю читателю пройти вместе со мной, шаг за шагом, теорию возникновения нашего физического мира, в котором мы существуем, со всеми его законами. Теорию возникновения и эволюции в том, что невозможно определить иначе, как Беспредельность.
1. Беспредельность, как фундаментальная реальность
Оглавление
Беспредельность не может быть определена в рамках формальной логики, так как любое определение автоматически делает определяемый предмет ограниченным, то есть предельным. Этот замкнутый круг формальной логики мы разрубим простой констатацией факта того, что формальная логика к Беспредельности неприменима. Но это не только не мешает нам дать понятное определение Беспредельности, но и положить его основным постулатом, на котором мы последовательно выстроим цельное здание теории.
Давая определение Беспредельности, мы производим ее формальное ограничение, редуцируем в некие пределы своего понимания. Но, с другой стороны, любое бытие в Беспредельности начинается с некоей первичной локализации, некоего частного ограничения, или первичного выбора.
Поэтому, давая определение Беспредельности, мы признаем, что определяем не саму Беспредельность, как таковую, а ту первичную субстанцию, в которой происходит эволюция нашего бытия, являющуюся следствием первичного ограничения, выраженного в том, что она существует.
Определение (01):
Беспредельностью называется то, что не имеет ограничений.
Основополагающий постулат:
Существует Беспредельность или то, что не имеет ограничений, кроме принципа своего существования.
В отличие от классических и иных современных физических теорий, нам достаточно только одного этого постулата, как фундамента для построения всего здания физики.
Начнем с того, что сформулируем и докажем три основные теоремы Беспредельности. По мере возможности там, где формальная логика применима, мы будем ее строго придерживаться. Там, где формальная логика не применима, мы будем это четко оговаривать и формулировать соответствующие применяемые принципы глобальной логики.
Теорема (т1):
Беспредельность, или то, что не имеет никаких ограничений, всеобъемлюще.
Доказательство:
Допустим, что есть нечто, что не охватывается Беспредельностью. В этом случае на Беспредельность накладывается ограничение, выраженное в том, что Беспредельность не охватывает это нечто. Это противоречит определению Беспредельности. Следовательно, теорему можно считать доказанной.
Теорема (т2):
Любая часть Беспредельности тождественна всей Беспредельности.
Эту теорему можно назвать «условием нелокализованности».
Для доказательства теоремы, докажем сначала следующее утверждение: то, что не имеет ограничений, не может быть ограничено в какой-либо своей части. Действительно, если в какой-либо части Беспредельности имеются некие ограничения, то из этого следует, что сама Беспредельность ограничена этими ограничениями в этой своей части, что противоречит определению Беспредельности.
Теперь учтем то, что Беспредельность не может быть ограничена условием локализации, или определением какого-либо места нахождения в каком-либо пространстве. Из этого следует вывод о том, что любая часть Беспредельности не может иметь приоритетности по отношению к самой Беспредельности, перед другими частями, так как любая шкала приоритетности являла бы собой определенное условие ограничения. Но тогда и сама Беспредельность не может иметь приоритета перед своей частью, так как части не могут являться чем-то «внутри» некоей объединяющей их Беспредельности, иначе они были бы ограничены этим условием. Таким образом, теорему можно считать доказанной.
Теорема (т3)
Любая часть Беспредельности симметрична относительно Беспредельности.
Доказательство:
Классический принцип симметрии предполагает тождественность частей относительно некоей выделенной позиции: точки, линии, плоскости... Но в нашем случае речь идет о симметрии относительно того, что само по себе не определено и не формализовано. Это тот случай, когда формальная логика в привычном виде неприменима. Однако нам для дальнейшего построения важно доказать то, что асимметрии любой части Беспредельности относительно другой ее части существовать не может. Если бы таковая асимметрия существовала, то это означало бы, что одна часть Беспредельности может быть формально разделена на части, имеющие различное отношение к другой части Беспредельности, что представляет собой выделяющий и огранивающий принцип, который не может существовать в Беспредельности по нашему определению.
Таким образом, теорему можно считать доказанной.
2. Вселенная, как локализация в Беспредельности
Оглавление
Физика, как наука, оперирует только тем, что может быть объективно измерено и соотнесено друг с другом. Можно ли измерить Беспредельность? Вопрос не корректный. Для измерения выбирают определенную меру и соотносят ее со всем остальным, аналогичным, этой мере. Из-за разнообразия физических проявлений, в физике применяются различные меры для различных групп явлений. Сама по себе мера, выбранная произвольно, не является как таковой физической величиной. Законы физики определяют соотношения, а не меру. Поэтому более корректен вопрос: с чем можно соотнести Беспредельность? Ответ прост - только с самой собой. Более того, все наши физические меры являются частями Беспредельности и, следовательно, по теореме (2) сами являются тождественными Беспредельности.
Но как возникли все физические отношения нашей объективной реальности, если соотносить Беспредельность с Беспредельностью можно бесконечно разнообразными вариантами, а мы имеем дело с конкретными и очень точными соотношениями и сочетаниями? Как получается так, что одна часть Беспредельности укладывается некое число раз в другой ее части, и при этом они тождественны?
Любое сочетание частей некоего целого накладывает этим сочетанием конкретное ограничение и мы приходим к парадоксу: все проявления бытия должны быть частями Беспредельности, но наличие сочетаний и отношений между ними ограничивает их и, соответственно, лишает возможности быть частями Беспредельности, которые в соответствии с теоремой (2), должны быть ей тождественными.
Этот парадокс неразрешим в пределах формальной логики. Проблема заключается в том, что формальная логика предполагает взгляд снаружи, вынесенный за пределы рассматриваемого объекта. Но относительно Беспредельности такого вынесенного взгляда не может существовать в принципе. Имеется только одна возможность существования взаимоотношений - внутренняя субъективность Беспредельности в любой из ее частей.
Внутренняя субъективность означает внутреннее самоограничение, на котором строятся все физические взаимоотношения ограниченного в самом себе мира.
Сам факт конечного соотношения различных частей физического мира говорит о том, что отношение Беспредельности к самой себе в нашей объективной реальности чем-то ограничено. Беспредельность, представляемая одной своей частью, укладывается некое ограниченное количество раз в другой своей части, то есть, в соответствии с теоремой (2) в самой себе и этим ограничивается. Такое ограничение может допускать только логика внутренней субъективности. Назовем это явление локализацией или локальным отражением Беспредельности самой в себе.
Определение (02):
Локализацией или субъективным отражением называется отражение Беспредельности в самой себе, ограниченное определенным конечным числом.
Учитывая, что Беспредельность обладает свойством симметрии, ограничение, как свойство локализации, должно быть симметричным и тождественным по всем ее проявлениям. Из этого необходимо следует вывод о том, что ограничивающее локализацию число должно быть только целым. Действительно, если бы локализация, как часть Беспредельности, отражалась бы сама в себе не целое число раз, то оставшаяся дробная или иррациональная часть сама являлась бы неким дополнительным ограничением, нарушающим общую симметрию.
Определение (03):
Основным числом локализации называется целое положительное число n, равное количеству отражений локализации самой в себе по любому из своих проявлений.
Таким образом, все процессы в локализации измеряются исключительно соотношением с основным ограничивающим числом и самой локализацией, как единицей. Именно такой локализацией является наша Вселенная, со всеми ее физическими законами, что мы далее и докажем конкретными расчетами. Более того, мы однозначно определим ограничивающее число нашей физической реальности и покажем, что именно оно является основой всех физических качеств и свойств нашей Вселенной. Внутренняя субъективность Вселенной для каждого из нас является внешним объективным миром с набором объективных физических законов, и это не противоречит принципу объективности физической науки.
В пределах субъективного ограничения локализации для каждого из ее внутренних проявлений все остальные внутренние проявления являются объективной окружающей реальностью с конкретными объективными соотношениями.
Свойство внутреннего самоограничения локализации можно назвать редукцией отражения. Оно не лишает локализацию каких-либо свойств Беспредельности, но добавляет к ним в своей собственной внутренней субъективной относительности условие безусловного ограничения основным числом.
То, что локализация отражается сама в себе определенное число n раз, по другому можно определить, как свойство измерения локализацией самой себя ограниченное число раз, в каждом из которых, она находит сама себя. Причем любая последовательность измерений по любому свойству будет не только ограничена основным числом, но и замкнута сама на себя, рис. 1, а).
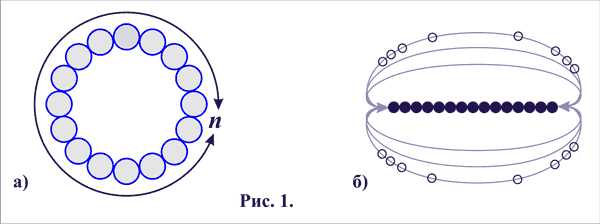
Рис. 1
Замкнутость цикла самоотражений следует из того, что все отражения тождественны и не могут иметь приоритета друг перед другом, то есть среди них не может быть ни первого, ни последнего.
Только необходимо иметь в виду то, что изображение на схеме последовательности отражений в виде круга не более чем условная схема, необходимая для наглядности. Наши привычки восприятия реальности в виде евклидового пространства не годятся для понимания Беспредельности, так как она не имеет тех ограничений, которые обуславливают евклидовое пространство. Замкнутость цикла не может иметь ни направления, ни линейной цепочки, ни, тем более, формы круга, рис. 1.б). Конечно, это изображение не менее условно, но важно понять сам принцип.
Поскольку локализация является ограниченным отражением Беспредельности по всем ее свойствам, в данном случае основное число n отражает такое понятие, как бесконечность.
Иными словами, основное число локализации есть ее относительная “бесконечность” по любому из возможных измерений (самоотражений), составляющая замкнутый цикл. При смещении в любой последовательности отражений на n+1 , первое в последовательности отражение перестает для нее объективно существовать. (04)
Единственной моделью, которую мы можем постараться себе представить, и которая отвечала бы этим свойствам локализации, является самозамкнутая сама на себя фрактальная структура, рис. 2).

Рис. 2
Каждый из кругов на данной схеме означает локализацию, отражающуюся в самой себе последовательным замкнутым циклом n раз, рис. 2.а). Поскольку каждое из отражений тождественно всей локализации в соответствии с теоремой (2), то внутри такого отражения она снова отразит себя аналогичным циклом из n раз. И так будет продолжаться это же самое число n раз, пока локализация не найдет сама себя в том отражении, с которого началась последовательность отражения в себе самой. Цикл отражений замкнется, а каждое фрактальное повторение будет тождественно остальным, и среди них не может быть ни первого, ни последнего. Аналогично сложится ситуация и когда локализация будет пытаться “выходить из себя”, отражаясь во “внешнем пространстве”, находя там сама себя это же самое число n раз, рис. 2.б).
Это свойство тождественности любого состояния локализации ей самой очень важно для понимания законов нашего физического мира, что будет показано далее.
3. Два основных состояния локализации: внутреннее и внешнее
Оглавление
Поскольку каждое из последовательных отражений локализации в самой себе в количестве n раз является самостоятельной объективной определенностью, назовем это элементарным состоянием локализации.
Определение (05):
Элементарным состоянием локализации называется одно из ее полностью тождественных отражений в самой себе.
Назовем набор всех элементарных состояний локализации - полным внутренним состоянием локализации.
Определение (06):
Полным внутренним состоянием локализации называется весь набор ее элементарных состояний по всему ее основному числу n, относительно одного из ее элементарных состояний.
А теперь зададимся вопросом: сколько всего своих внутренних элементарных состояний имеет локализация? Или по-другому: сколько раз локализация отразится сама в себе?
Поскольку любая внутренняя последовательность состояний в локализации ограничена ее основным числом n, то, естественно, при последовательном измерении (отражении) самой себя локализация найдет себя n раз. Но, учитывая теорему (3), локализация, как часть Беспредельности, должна быть симметрична внутри себя. Следовательно, локализация, отражаясь сама в себе, не может ограничиться одной последовательностью отражений. Такая последовательность, будучи единственной, нарушила бы симметрию. Закон симметрии требует полного замкнутого цикла из n последовательностей (замкнутых циклов) самоотражений. Таким образом, мы получаем n циклов по n или n2 внутренних элементарных отражений локализации в самой себе.
Вывод (07):
Полное состояние локализации состоит из n2 своих внутренних элементарных состояний.
Это означает двумерность внутреннего пространства реальных элементарных состояний локализации.
Вывод (08):
Локализация двумерна по пространству своих реальных внутренних состояний, которое представляет собой неевклидовую двумерную структуру, замкнутую по каждому из своих двух измерений.
Далее отметим, что исходя из теоремы (3) локализация, как отражение Беспредельности, должна быть симметрична относительно самой Беспредельности. Любая определенность в Беспредельности нарушает симметрию. Следовательно, каждая определенность должна необходимо иметь свое симметричное дополнение относительно Беспредельности, рис. 3).

Рис. 3
Для любого полного внутреннего состояния локализации А должно существовать А (не А) отвечающее следующим уравнениям:
1) |А|=|А| = n2
2) А + А=0
Назовем все n2 элементарных состояний А -
внешними состояниями локализации.
Запишем уравнения для элементарных внутренних и внешних состояний:
3) |а|=|а|=1 , где а - внутреннее элементарное состояние локализации, а а - внешнее элементарное состояние локализации, как симметричное относительно Беспредельности дополнение.
4) а + а =0
Уравнения 2) и 4) означают то, что в Беспредельности любая локализация существует только для самой себя и своего отрицания (дополнения до целого) и никаким образом не отражается в иных локализациях.
Все внешние состояния а точно так же равны между собой, как и внутренние состояния а , то есть представляют собой замкнутую неевклидовую двумерную структуру, одинаково отражающуюся относительно каждого из состояний.

Рис. 4
На рис. 4) условно изображена симметрия полного внутреннего и полного внешнего состояний локализации друг к другу относительно Беспредельности. С позиции А, рис. а) , полное состояние А для нее является внешним. На рис. б) изображена та же самая симметрия, но уже с позиции А , так как А и А полностью тождественны.
Исходя из теоремы (2), каждое полное состояние локализации относительно каждого ее элементарного состояния равнозначно и тождественно. Из этого следует, что при измерении относительно каждого элементарного состояния а , существует полное состояние локализации из всех своих n2 внутренних элементарных состояний а и n2 внешних элементарных состояний а , рис. 5).
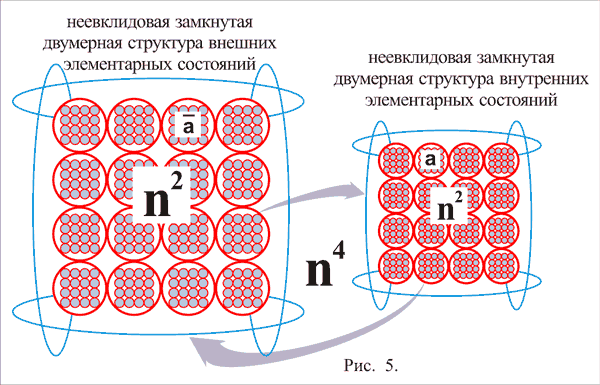
Рис. 5
Таким образом, получается, что полное число внутренних и внешних элементарных состояний локализации составляет n4 .
Пространство всех этих состояний представляет собой неевклидовую самозамкнутую четырехмерную структуру. Определение “самозамкнутая” не может быть заменено определением “замкнутая” потому, что даже обычный евклидовый куб является замкнутым относительно своего внутреннего пространства. Данная неевклидовая четырехмерная структура является замкнутой не только для своего внутреннего пространства, но и для внешнего, то есть для всего, что так или иначе в ней отражается и с ней связано. Представить это наглядно и проиллюстрировать в привычной для нас трехмерной логике пространственного восприятия невозможно. Наше восприятие и, основанное на нем, воображение сформировались в очень малом сегменте этого неевклидового пространства, в котором оно редуцируется в евклидовое, и охватить его целиком не могут.
Обращаем внимание на то, что мы путем логического анализа, исходя из основополагающего постулата о Беспредельности, пришли к выводу о том, что пространство объективного физического бытия представляет собой самозамкнутую неевклидовую четырехмерную структуру, которая в локальной редукции представляет собой наше привычное трехмерное пространство с четвертым измерением времени.
Таким образом, нам удалось раскрыть одну из основных тайн нашего физического бытия, заключающуюся в факте трехмерности физического пространства.
Определим свойства этой неевклидовой самозамкнутой четырехмерной структуры:
1-е свойство - внутренняя тождественность:
Исходя их теоремы (2) любое элементарное состояние тождественно всем остальным. (09)
2-е свойство – внутренняя симметрия:
Исходя из теоремы (3) данная структура должна быть симметрична относительно любого элементарного состояния, то есть она симметрична в любой своей точке, а в совокупности с первым свойством это означает, что любое элементарное состояние в своей относительности находится в центре данной структуры. (10)
Пользуясь понятиями современной физики, второе свойство можно назвать свойством относительности центра структуры в системе отсчета, связанной с любым из элементарных состояний.
Из этого принципа относительности центра структуры следует, что расстояние в любую сторону от любого из элементарных состояний одинаково и равно n. Это свойство в привычной для нас евклидовой логике соответствует шару, и размер n можно было бы рассматривать, как радиус, если бы объем этой структуры не равнялся n4, что соответствует четырехмерному кубу со стороной n. С другой стороны, если бы это был четырехмерный шар, то его максимальный поперечный размер не превышал бы n, и получается, что его
радиус равен диаметру. Как бы это не казалось странным, но это именно так, и это фундаментальная логика локализации в Беспредельности. Независимо от того, как мы себе представляем эту неевклидовую объемную структуру: шаром или кубом,
его размер, измеренный изнутри в любую сторону, и полный размер снаружи одинаковые. (11). Можно было бы эту странную объемную фигуру назвать “кубошаром”, но все же это в первую очередь куб, так как в небольшой локальной своей части он редуцируется в привычное для нас евклидовое пространство трех физических измерений и четвертого измерения времени, представляющие собой кубическую структуру. Однако во внешнем с ним взаимодействии создает иллюзию шара с диаметром, равным его стороне. В глобальном неевклидовом пространстве не существует таких явлений, как круг или шар. Не существует ни окружности, ни диаметра, ни их отношения друг к другу, которое в нашем редуцированном евклидовом пространстве мы привыкли обозначать числом
"Пи" .
Вся наша Вселенная, как локализация в Беспредельности, и любая элементарная частица, как тождественное ее отражение самой в себе, представляют собой именно такую неевклидовую самозамкнутую четырехмерную структуру. Поскольку мы привыкли их размер называть радиусом, то, отдавая дань традиции, мы будем и далее называть основной размер n по каждому измерению этой структуры - радиусом.
Вывод (12):
Радиус внутренних процессов элементарных состояний локализации равен их внешнему размеру во внешних сочетаниях и процессах.
Назовем весь спектр возможных внутренних и внешних состояний локализации - базовой матрицей состояний локализации.
Определение (13):
Базовой матрицей состояний локализации называется полный объем внешних и внутренних состояний локализации, представляющий собой самозамкнутую неевклидовую четырехмерную структуру радиуса n (основного числа локализации) и объема - n4.
4. Время и пространство
Оглавление
Как мы уже показали, статически все n4 элементарных состояний базовой матрицы полностью тождественны. Но наше физическое объективное бытие представляет собой динамику последовательности состояний. Все последовательности в базовой матрице не имеют ни начала, ни конца, но мы каким-то образом сделали свой выбор одного первого состояния, с которого и началась наша эволюция. Сам принцип производства выбора сознанием в физике не рассматривается, но физика, основываясь на практических данных, породила теорию «Большого Взрыва», которая предполагает некую начальную точку отсчета. В полном согласии с этой теорией и наша теория предполагает начальный момент отсчета - полное состояние локализации относительно некоего выбранного элементарного состояния, которое становится начальным в эволюционной последовательности. И для дальнейшего исследования
не важно, как был произведен этот выбор, важно то, что этот выбор являет собой нарушение симметрии локализации. Это первичное нарушение симметрии порождает цикл необходимости восстановления симметрии.
Важно понять, что цикл необходимости есть наш внутренний относительный процесс, а вся локализация целиком всегда симметрична.
Определение (14):
Циклом необходимости называется процесс восстановления симметрии,
нарушенной первичным выбором, объективно существующий только относительно
данного выбора.
Таким образом, цикл необходимости - это неумолимый процесс предзаданный самим актом выбора в своих конечных характеристиках полного цикла. Это главная фундаментальная основа всех физических процессов и сил объективного физического мира, реализованного в базовой матрице локализации. (15)
Суть цикла необходимости в том, что выбранное полное первичное состояние локализации, со всеми своими элементарными состояниями, необходимо и последовательно переходит по полному циклу внешних состояний n. Поскольку внешние состояния представляют собой двумерную структуру, то направление последовательности цикла определяется случайным выбором.
Таким образом, моментом первичного выбора, определяется n2 реальных внутренних состояний локализации в одном первичном внешнем состоянии. Все остальные n2 внешних состояний относительно начального момента выбора являются потенциальными. Последовательный переход всех реальных состояний по внешним, потенциальным, являет собой время.
Определение (16):
Временем называется последовательность сменяющих друг друга реализованных полных состояний локализации в их смещении по двумерной структуре потенциальных внешних состояний под воздействием цикла необходимости.
Определение (17):
Одномоментным состоянием называется каждое реализованное полное состояние локализации в последовательности времени.
В соответствии с размером локализации, последовательность времени состоит из n одномоментных состояний и замкнута.
Но внешние потенциальные состояния локализации представляют собой структуру двух измерений без какого-либо выделенного направления. В каком направлении будет двигаться последовательность реализованных состояний локализации?
Двумерная структура внешних состояний является неевклидовой. Оба ее измерения представляют собой самозамкнутые циклы полностью тождественных состояний, а полное количество ее состояний равно n2, что и определяет ее площадь.
Непривычная нам логика этой двумерной структуры в том, что любая ее точка является центром, а максимальное расстояние, которое может быть измерено в любом направлении равно n.
Все направления этой двумерной структуры тождественны и равноправны. Поэтому нарушение симметрии первичным выбором одинаково отражается по всем направлениям одновременно. Соответственно и цикл необходимости должен устремлять последовательность переходов реализованных полных состояний во все стороны одновременно, то есть, распространяться по площади внешних элементарных состояний, рис. 6).
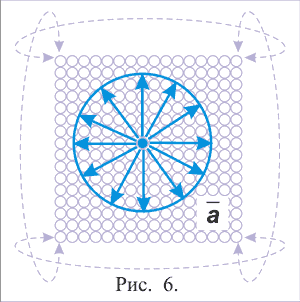
Рис. 6
Но как это согласовать с тем, что мы имеем при этом направленную замкнутую последовательность n одномоментных состояний?
Попробуем определить границы исследуемому явлению. Во-первых, это должна быть направленная последовательность в случайно выбранном направлении. Во-вторых, каждый элемент последовательности должен представлять собой площадь внешних элементарных состояний. В-третьих, движение по каждому из двух измерений должно быть тождественным в отношении принципа восстановления симметрии, что означает одинаковую скорость движения в сторону дополняющей противоположности.
Совместить эти условия можно только в модели, когда полное состояние локализации последовательно смещается в случайно выбранном направлении по двумерной структуре внешних состояний от начальной единицы до n, одновременно расширяясь с той же скоростью по второму измерению структуры внешних состояний к измерению выбранного направления. То есть, от состояния нарушенной симметрии, до состояния ее полного восстановления, рис. 7).

Рис. 7
Последовательностью времени в этом случае будет случайно выбранное направление (измерение) двумерной структуры внешних состояний, а одномоментным будет площадь сегмента с единичной стороной по измерению времени и стороной, равной n1 пройденным моментам времени по второму измерению двумерной структуры внешних состояний. Обозначим одномоментный промежуток времени Dt как dt . Таким образом, количество одномоментных внешних состояний, соответствующих полному реализованному состоянию локализации в момент времени t = n1dt будет равно n1 , рис. 8).

Рис. 8
Поскольку оба измерения двумерной структуры внешних состояний являются тождественными, направление последовательности выбрано случайным образом, а одномоментные внешние состояния располагаются в плоскости этих двух измерений, то вся эта двумерная структура и являет собой время.
Определение (18):
Плоскостью времени называется двумерная структура потенциальных внешних состояний, в которой производится случайный выбор направления последовательности времени.
В плоскости времени располагаются потенциальные внешние состояния, в которых реализуются n2 реальных внутренних одномоментных состояний. Таким образом, одномоментное состояние в плоскости времени представляет собой площадь потенциальных элементарных состояний.
Определим направление последовательности времени как измерение физического времени, а дополнительное к нему измерение плоскости времени как потенциальное измерение времени.
Определение (19):
Измерением (вектором) физического времени называется измерение плоскости времени, в направлении которого движется последовательность одномоментных полных состояний локализации.
Определение (20):
Измерением (вектором) потенциального времени называется второе измерение плоскости времени, дополнительное к выбранному в качестве физического времени.
В каждом последующем состоянии последовательности одномоментных состояний, начиная с первого, локализация реализует свое полное состояние в потенциальном пространстве внешних состояний. Таким образом, вся локализация состоит из своей реализованной и еще нереализованной частей. Реализованная часть это то, что уже объективно существует, а потенциальная часть - то, что только предполагается к существованию в будущем.
Определение (21):
Реализованной или материальной составляющей локализации на определенный момент времени называется весь объем элементарных состояний, пройденных локализацией в своем движении по циклу необходимости на этот момент времени.
Определение (22):
Динамической составляющей локализации называется весь объем ее элементарных состояний полного одномоментного состояния, двигающийся по вектору физического времени.
Определение (23):
Нереализованной составляющей локализации называется весь объем внешних, еще не реализованных в последовательности времени, элементарных состояний.
Обращаем внимание на то, что динамическая составляющая является частью реализованной составляющей локализации.
В каждом одномоментном промежутке времени всегда присутствуют n2 реальных внутренних состояний локализации, каждое из которых проецируется на n1 потенциальных элементарных состояний по измерению потенциального времени, образующие вместе трехмерную структуру динамической составляющей локализации. Это и есть то физическое трехмерное пространство, в котором происходят все физические процессы и взаимодействия, к которому мы привыкли в своей локальной и относительно малой части Вселенной.
Определение (24):
Физическим пространством называется пространство двух реальных внутренних измерений и одного потенциального измерения времени динамической составляющей локализации, которые в сумме составляют три взаимно-тождественных измерения.
Процесс восстановления симметрии, нарушенной первичным выбором, должен совершенно симметрично проходить не только по всей плоскости потенциального времени, но и по двумерной структуре реальных состояний, иначе он сам нарушал бы симметрию локализации. Но двумерная структура реальных внутренних состояний неизменно состоит из n2 своих элементарных состояний. Поскольку скорость смещения по циклу по всем четырем измерениям должна быть одинаковой, это означает, что
размер реального состояния по каждому измерению двумерной структуры реальных состояний постоянно растет в точном соответствии с ростом размера по вектору потенциального времени. То есть, размер реального элементарного состояния по всем трем измерениям физического пространства одинаков и увеличивается по ходу времени.
По вектору физического времени мы воспринимаем одномоментно только одно единственное состояние, в котором укладываются по n состояний по каждому из остальных трех измерений (всего n3 ) на отрезке равном пройденному времени, рис. 9).
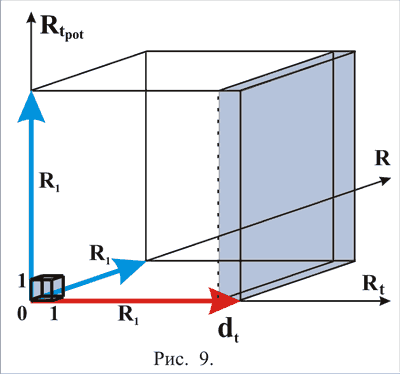
Рис. 9
Для простоты на рисунке изображен не четырехмерный, а трехмерный куб, с одним измерением физического времени Rt , вторым измерением потенциального времени Rtpot и третьим измерением реального внутреннего состояния R . Предполагается наличие еще одного измерения реального внутреннего состояния, являющегося четвертым к изображенным трем, но его изобразить сложно, как и то, что данная четырехмерная структура неевклидовая и самозамкнутая.
Динамической составляющей является только сегмент куба, соответствующий одномоментному промежутку dt по вектору физического времени на момент времени t1 = n1dt. Поскольку все измерения четырехмерного пространства состояний локализации тождественны, то промежуток, пройденный динамической составляющей по вектору физического времени, можно определить и как промежуток пространственной протяженности.
Определение (25):
Единицей пространственной протяженности называется размер пространственной протяженности по вектору физического времени dr , соответствующий одному одномоментному промежутку dt .
Таким образом, за время t1 = n1dt динамическая составляющая прошла пространственный промежуток:
R1 = n1dr
Обозначим скорость движения динамической составляющей по вектору физического времени - c , которая равна:
c = dr /dt .
Поскольку все измерения тождественны, и цикл необходимости развивается с одинаковой скоростью по всем из них, размер R1 = n1dr динамической составляющей на каждый момент времени по всем измерениям и всем возможным направлениям будет одинаковым.
Теорема (т4):
Ни одно состояние локализации не может двигаться со скоростью большей скорости движения динамической составляющей локализации по циклу необходимости c = dr /dt .
Это следует из того, что локализация последовательно по циклу необходимости находит сама себя (измеряет собой) в определенном количестве элементарных состояний, что и является ее динамической составляющей, и ни одно ее реальное состояние не существует вне нее, следовательно, не может ее опередить.
Стоит сразу отметить то важное обстоятельство, что момент времени, когда локализация может точно определить свои элементарные состояния, то есть измерить себя, всегда равен одному элементарному состоянию по измерению времени dt , или целому числу таких состояний.
Любые попытки измерений последовательности процессов в меньшем dt промежутке времени будут относительны и давать условно-вероятностный результат. Это связано с тем, что в
меньшем dt промежутке времени все события не связаны строгой последовательностью и являются одномоментными. Аналогично и с единичным пространственным промежутком dr .
Это минимальный размер пространственной протяженности, который может быть измерен с однозначным результатом. Измерения размеров меньших, чем этот пространственный промежуток, возможны только как статистически усредненные в рамках той или иной вероятности, зависящей от способа измерения.
Дополнительно запишем следующие отношения:
Rn = ndr , где Rn - размер всей локализации, включающий ее реализованную и потенциальную составляющие, и соответствующий радиусу полного потенциального поля всех состояний базовой матрицы локализации.
Tn = ndt , где Tn - время полного цикла локализации.
5. Степени базовой матрицы
Оглавление
Мы показали, что наша Вселенная, как локализация в Беспредельности, должна иметь свое основное ограничивающее число. Но как возникает это число ограничения локализации? Чтобы ответить на этот вопрос, сначала задумаемся, а что будет дальше с локализацией, когда цикл необходимости восстановления симметрии, нарушенной первичным выбором, будет исчерпан до конца? На первый взгляд, просится ответ о том, что весь цикл повторится в обратную сторону, как маятник или иной циклический процесс из привычной для нас физической картины мира. Но это не так.
Чтобы понять, как процесс пойдет дальше, следует в первую очередь обратить внимание на очень важный нюанс. Первичным выбором порождается процесс, который является реальной объективной данностью, но
вся остальная часть матрицы потенциальных состояний, в которой процессу еще только предстоит развиваться, является внутренней производной уже идущего процесса, то есть вне него не существует. Другими словами, это нематериальная проекция своего внутреннего развития в будущее, нечто ожидаемое, но само по себе еще не существующее. Каждое потенциальное состояние начинает реально существовать с того момента, когда процесс достигает его.
Но что происходит с теми потенциальными состояниями, которые процесс уже прошел и оставил позади? С точки зрения процесса - это прошлое, но для самой локализации нет ни прошлого, ни будущего, ни начала, ни конца. Течение времени - всего лишь наш относительный выбор некоего случайного направления.
Поэтому для локализации все пройденные процессом состояния продолжают существовать без какого-либо приоритета друг перед другом.
Таким образом, когда процесс завершается, мы имеем полностью заполненную реализованными реальными элементарными состояниями базовую матрицу. Но ведь это же снова нарушает симметрию в Беспредельности!
Реализованная в полноте цикла базовая матрица в свою очередь становится начальным состоянием нового цикла необходимости.
И самое главное в этом то, что все состояния предыдущей базовой матрицы становятся одномоментными в первом начальном моменте времени новой, последующей матрицы.
Весь цикл времени предыдущей матрицы, все последовательные состояния от прошлого к будущему, превращаются в одномоментные, полностью тождественные друг другу состояния в новой более обширной матрице. (26).
Соответственно мы получаем, что реальных внутренних состояний в новой базовой матрице n4, а ее размер равен n2.
Но если числовой размер последующей по развитию процесса матрицы равен квадрату числового размера предыдущей, то этот же самый принцип мы можем проследить и в начало развития процесса по матрицам. То есть, если последовательно извлекать квадратный корень из числового размера матрицы, то неминуемо придем к некому минимальному начальному числу, первичному импульсу, породившему весь процесс.
Так сколько же реальных состояний мог иметь первичный импульс? Сколько раз он отражал себя внутри себя? Очевидно, что такое число должно быть минимальным и самым простым, так как вероятность случайного возникновения процесса тем выше, чем меньше и проще число его определяющее.
Возникновение процесса, минимально разделенного всего на две части, наиболее вероятно.
Более того, сам процесс разделения является актом, делящим сначала на две части, а уже потом на большее количество, если процесс деления повторяется.
Но если акт деления на две части свершился, то необходимо возникает и весь цикл восстановления симметрии, в котором уже повторное случайное разделение столь мало вероятно, что уже не может на него повлиять.
Есть еще единица, но локализация из одного элементарного состояния не может существовать, так как она не может быть симметричной относительно Беспредельности. Любая единица, как некое цельное состояние, если бы и возникло в Беспредельности, то тут же породило бы симметричное себе дополнение и возник бы цикл восстановления симметрии. Именно это и происходит при любом первоначальном импульсе, возникшем в результате случайной флюктуации в Беспредельности.
Первичный импульс порождает свое симметричное дополнение, как свою неотъемлемую внутреннюю составляющую. Таким образом, первичный импульс самим фактом своего появления в Беспредельности являет собой локализацию основного числового размера 2. (27).
Соответственно, и базовая матрица первичной локализации имеет размер 2. С нее и начинается процесс эволюции по следующим друг за другом циклам необходимости.
Определение (28):
Элементарной локализацией называется локализация числового размера 2.
Определение (29):
Первичной базовой матрицей называется базовая матрица элементарной локализации.
Такая первичная матрица имеет:
- числовой размер: n = 2 ,
- количество реальных внутренних элементарных состояний: n2 = 22 = 4 ,
- полное количество всех элементарных состояний матрицы: n4 =24 =16 .
- время полного цикла: Tn = ndt = 2dt .
Таким образом, полный цикл необходимости начальной локализации будет состоять всего из двух одномоментных состояний: свернутого нахождения всех четырех реальных элементарных состояний в пределах одного внешнего элементарного состояния, и второго состояния - полностью завершенного и реализованного по всей матрице цикла необходимости.
Математически формально такую первичную матрицу локализации можно назвать матрицей первой степени, и обозначить ее размер как n = 21 =2 .
Полная математическая формула размера локализации в последовательности степеней усложнения базовой матрицы выглядит так:
n = 2(2k-1), где k - степень первичной локализации (стадии усложнения).
Рассчитаем размер локализаций первого порядка значений k:
А(1): n = 2 ,
А(2): n = 4 ,
А(3): n = 16 ,
А(4): n = 28 = 256 ,
А(5): n = 216 = 65536 ,
А(6): n = 232 = 4294967296 ,
А(7): n = 264 = 18446744073709551616 ,
А(8): n = 2128 = 3,40282366920938*1038 ,
А(9): n = 2256 = 1,15792089237316*1077 ,
А(10): n = 2512 = 1,3407807929942*10154 ,
Как видим, увеличение размера происходит так быстро, что нет смысла просчитывать дальше. В следующих главах мы определим степень базовой матрицы нашей Вселенной и покажем, что седьмая степень слишком мала для нашей Вселенной, а девятая слишком большая. А вот восьмая степень числа n = 2128 совпадает просто идеально со всеми известными науке параметрами нашей Вселенной.
Рис. 10) иллюстрирует последовательность развития импульса по базовым матрицам:
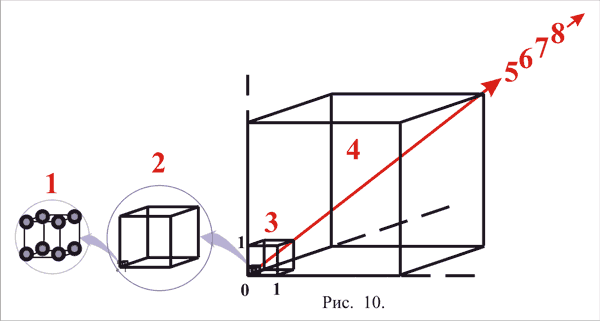
Рис. 10
Отметим одно важное обстоятельство. Наше логическое построение привело нас к тому, что
числовой размер локализации является ее базовой характеристикой только на период одного цикла необходимости и меняется скачкообразно в процессе ее эволюции. (30)
По ходу нашего рассуждения следует отметить еще один важный нюанс. Наша числовая логика требует, чтобы числовой шаг последовательности степеней базовой матрицы был одинаковым для любой локализации, порожденной любой случайной флюктуацией, а это уже само по себе накладывает ограничение на Беспредельность и противоречит главному постулату. Из этого необходимо следует вывод о том, что числовая логика нашего мира является следствием условия первичной субстанции, начального ограничения Беспредельности, определившего сам принцип нашего существования в ней. Но это всего лишь индивидуальная особенность принципа нашего существования, и не может распространяться на все эволюционные процессы любых случайных флюктуаций в Беспредельности. Этот очень важный вывод помогает нам понять всю глубину Беспредельности, но не может помешать нашим рассуждениям в рамках числовой логики, так как мы выстраиваем теоретическую картину исходя из данности принципа нашего существования, в котором эта числовая логика присутствует как основа.
Поскольку скорость движения по циклу необходимости равна:
c = dr /dt ,
а для цикла в последующей матрице одномоментный промежуток времени равен ndt и соответствующий ему единичный размер пространственной протяженности ndr , то скорость в последующем цикле не изменится:
c = ndr / (ndt ) = dr /dt = const.
Это означает, что скорость движения локализации по циклу эволюции является универсальной постоянной не только для одного цикла, но и по всей последовательности базовых матриц. (31)
Далее >>> гл. 6 - 11 >>> гл. 12 - 17
Оглавление
|












